O Histograma é, como o próprio nome sugere, uma ferramenta que nos ajuda a analisar o passado (a história) de nossos processos. Por isso, ele é uma daquelas ferramentas que atendem bem a proposta do nosso querido Deming, afinal “Quem não mede não gerencia”.

Isso porque, ao compreender o passado, conseguimos identificar padrões, acessar erros e compreender melhor nosso estado atual, nosso “contexto da organização”. Dessa forma, conseguimos traçar novos rumos, resolvendo problemas, evitando reincidências e moldando nosso futuro.

Além disso, para nós, essa metodologia tem um charme a mais, pois o Histograma é uma das 7 Ferramentas da Qualidade. Ele nos ajuda a agrupar e entender grandes grupos de dados, tornando mais fácil a interpretação da história dos seus processos. Ao longo deste conteúdo, inclusive, vamos entender porque essa ferramenta faz parte das 7 clássicas.

Enfim, por esses e diversos outros motivos, o Histograma é tão importante e se faz presente em tantas empresas mundo afora. Assim sendo, criamos mais um SUPER ARTIGO para você. Aqui, você vai entender como essa ferramenta foi criada, para que ela serve e como aplicá-la. Esse é mais um daqueles conteúdos em que você aprende mais e que pode usar para treinar sua equipe! 😉

Então, para começar, vale a pena assistir nosso vídeo no YouTube também. Basta clicar abaixo e adentrar no universo do Histograma, e da Gestão da Qualidade. Veja:

Conhecendo a história do Histograma (e seu “criador”)

A história desta ferramenta tem, digamos, peculiaridades interessantes. Digo isso porque ela foi utilizada muito antes de receber um nome.

Voltaire, por exemplo, já dividia dados em categorias lá no século 17 (1601 a 1700). William Playfair usava algo similar ao histograma para apresentar importações e exportações na Escócia em 1781. Florence Nightingale, enfermeira britânica, usou gráficos de barras para persuadir o governo britânico a melhorar a higiene nas linhas de frente do exército por volta de 1850. Isso sem contar diversos prováveis usos não registrados.

Entretanto meus amigos, uma das primeiras utilizações “oficiais” do termo Histograma ocorreu pela primeira vez em 1883, utilizado pelo advogado e estudioso em estatística francês André-Michel Guerry. Na época, ele o utilizou em sua análise estatística sobre o histórico de crimes ocorridos em Paris. Entretanto, aparentemente, ele utilizou o termo “historical diagram” e posicionou as variáveis no que mais tarde ficaria conhecido como mapa coroplético. Um mapa que usa cores ou padrões para mostrar como um dado estatístico se distribui em diferentes regiões.

De qualquer forma, em 1895, o matemático britânico Karl Pearson introduziu a palavra “Histograma” em suas palestras sobre estatística, utilizando-a como um termo para uma forma comum de representação gráfica. Isto é, um gráfico cartesiano com dados e frequências (já já eu explico melhor 😉). Como ele foi o primeiro a cunhar o termo (de maneira oficial), Karl Pearson é considerado, por muitos e até hoje, o criador do Histograma!

O que é um Histograma?

Explicando de forma teórica, o Histograma (conhecido também como Gráfico de Distribuição de Frequências), é uma representação gráfica para a distribuição de dados quantitativos de acordo com a frequência em que ocorrem. Assim, de forma prática e simples, ele cruza dois tipos de informações:

• Frequências e intervalos: a quantidade de vezes que algo ocorre em um intervalo de classes (também chamadas faixas);
• Objeto de análise (também chamada “Variável de interesse”): os dados que serão analisados em suas ocorrências já coletadas.

Dessa forma, conseguimos entender melhor com que frequência o objeto de análise acontece dentro de uma determinada faixa de análise. Parece complicado, eu sei, mas a mágica do Histograma é transformar isso tudo em algo muito simples! Calma que já eu mostro os exemplos e aí tudo vai ficar claro!

De qualquer forma, o importante é entendermos que, com essa ferramenta, conseguimos transformar uma tabela de frequências em um gráfico de barras. Isso vai facilitar, por exemplo, visualizarmos o comportamento, a variação e os padrões de um processo. Vale ressaltar, também, que podemos usar o Histograma tanto para processos que entregam produtos quanto na prestação de serviços.

Além disso, como já dito anteriormente, essa ferramenta é tão importante que foi incorporada à curadoria das 7 Ferramentas da Qualidade. Coletânea essa reunida por Kaoru Ishikawa na década de 50 e peça chave da Qualidade e da história da área!

Vantagens de utilizar o Histograma

Ao longo do texto, vou sempre reforçar e explicar as vantagens de usar essa ferramenta, mas como de costume, gosto de deixar uma lista didática sobre o assunto. Ela nos ajuda a fixar melhor o conteúdo e orientar o pensamento! Então, entre as vantagens do Histograma estão:

• Rapidez e simplicidade de coleta e elaboração do gráfico;
• Visualização fácil da quantidade de itens por faixas (intervalos);
• Simplicidade ao compreender a distribuição geral dos dados;
• Facilidade na identificação de anomalias e comportamentos fora do esperado (erros, defeitos, não conformidades, etc);
• Representação gráfica e visual da variação de um processo ou tarefa;
• Apresentação de uma base sólida para comparações “antes e depois” da implementação de melhorias;
• Maior facilidade de se comunicar e conseguir o engajamento das equipes;
• E por aí vai!

Como funciona um histograma?

De forma simples, temos um gráfico cartesiano com dois eixos: os famosos X e Y. Geralmente, no eixo Y colocaremos a frequência com que os dados foram coletados. Já no eixo X colocaremos, então, as faixas do objeto de análise (nossa variável de interesse e os dados coletados).

Escrevi “geralmente” ali em cima, pois encontrei também fontes que dizem que você pode construir o gráfico invertendo os eixos. Ou seja, Y para dados e X para frequência. Me parece estranho e confesso que nunca vi usar assim, mas como não conheço todos os contextos do mundo, achei que valeria a pena citar aqui. Se seu processo não tiver nenhuma especificidade, use da maneira tradicional, pois a interpretação, repito, me parece mais fácil.

Enfim, resumindo, vamos juntar os dados coletados no eixo X e as frequências de ocorrência no Eixo Y. O resultado será um gráfico que agrupa os resultados em barras, facilitando sua análise e visualização.

Interpretando um Histograma

Para facilitar o entendimento, vejamos uma interpretação de um Histograma. Ao fazer isso, compreenderemos como cada dado se comporta em relação à sua frequência.

Imagine que há um limite de tamanho para a produção de uma determinada peça. Assim, ao fazermos a medição, chegamos à conclusão de que algumas peças ficaram alguns milímetros fora do padrão desejado. Para especificar, imagine que de 10 mil peças produzidas, 500 apresentaram divergência.

Depois, agrupamos as 500 peças não conformes de acordo com os milímetros fora do padrão, dentro de faixas de defeito. Por exemplo, peças com dimensões erradas entre “2 e 3 milímetros”. Assim, teríamos um gráfico parecido com este:

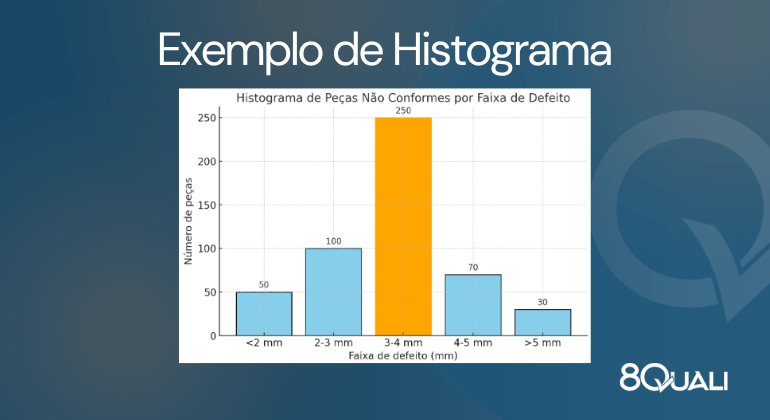
Ao analisar esse gráfico, por exemplo, poderíamos chegar a conclusões como:

1. A maior faixa de não conformidades está entre 3 e 4 milímetros (250 peças) – abaixo sinalizado em vermelho;
2. 350 peças têm erros entre 2 e 4 milímetros (100 unidades entre 2 e 3 mm; mais 250 unidades entre 3 e 4 mm) – abaixo sinalizado em azul;
3. A minoria dos erros corresponde às maiores divergências de tamanho (50 peças menores que 2 mm e 30 peças maiores que 5 mm) – abaixo sinalizado em verde claro.

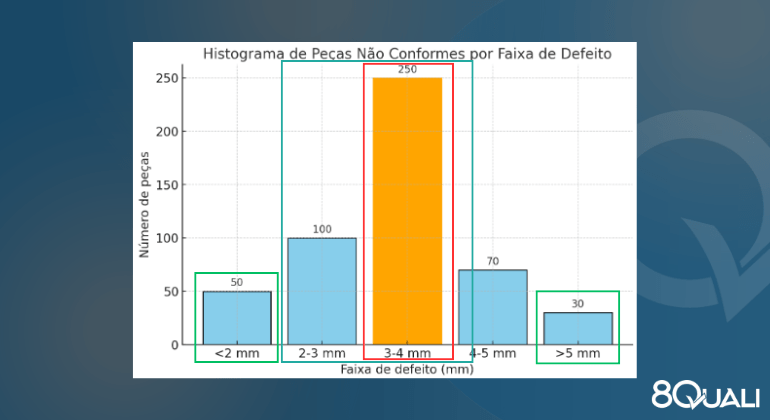
Entendendo LIMITE INFERIOR e LIMITE SUPERIOR

No meu gráfico, coloquei faixas exatas: entre 2 e 3, entre 3 e 4, etc. Fiz isso porque é mais didático e facilitaria sua compreensão. Porém, lembre-se: os números não podem se “repetir” no gráfico. Isso significa que:

• a faixa <2 é composta de números maiores ou iguais a 0 e menores que 2 ([0, 2[), e nunca será 3;
• Já a faixa 2-3 é composta de números maiores ou iguais a 2 e menores que 3 ([2, 3[), mas nunca chegando a 3;
• da mesma forma, a faixa 3-4 é composta de números maiores ou iguais a 3 e menores que 4 ([3, 4[), nunca chegando a 4;
• e por aí vai!

A esses intervalos damos o nome de Limite Inferior (que será sempre IGUAL ou MAIOR que…) e de Limite Superior (que será sempre MENOR que…). Por exemplo, na faixa 4-5, o Limite inferior é 4 (então, números iguais ou maiores que 4) e o Limite Superior é 5 (então, números menores que 5). 😉

Entendendo frequência ABSOLUTA ou RELATIVA

Além disso, meus amigos, a frequência pode ser Absoluta ou Relativa, algo bastante simples, mas vale explicar. Vejamos:

• Frequência Absoluta (FA) é o dado bruto que coletamos (“250 peças apresentaram desvio entre 3 e 4 milímetros”);
• Frequência Relativa (FR) é a porcentagem em relação ao total de dados coletados (“2,5% das peças apresentaram desvio entre 3 e 4 milímetros).

Habitualmente, não existe certo ou errado. Ambas são úteis e mostram o “mesmo resultado”, porém sob perspectivas diferentes.

Entretanto, a título de insights, vale usar a Frequência Absoluta quando o público-alvo precisa ver números reais. Conversando com a produção, por exemplo, dizer “Foram 250 peças não conformes” soa mais concreto que “2,5% da produção está não conforme”. Ou seja, pode ser útil em análises operacionais (pois a quantidade influi na tomada de decisão). Talvez valha usá-la, também, quando o total de dados é importante (algo como“200 medições” em uma auditoria de processo”).

Já a Frequência Relativa é útil em apresentações gerenciais, pois percentuais comunicam melhor e nem todo gestor gosta de números específicos. Também é interessante quando o tamanho da amostra não é o foco, mas sim a proporção (por exemplo: “70% dos chamados foram resolvidos em até 10 minutos”).

Também é interessante usar FR ao comparar amostras diferentes. Imagine analisar tempo de atendimento de 35 clientes ontem ao tempo de 80 clientes hoje. Ao usar FA, pode parecer que um grupo teve mais relevância porque a amostra é maior (80 contra 30), o que pode não ser, necessariamente, verdade. Entretanto, usando percentuais (%), a comparação foca realmente no tempo de atendimento.

Como montar o gráfico do Histograma?

O Histograma é uma ferramenta relativamente fácil de ser executada. Mesmo que ele seja uma ferramenta estatística, é possível construí-lo de forma mais fácil, possibilitando, assim, seu uso mesmo sem grandes conhecimentos em cálculo.

Obviamente, há usos avançados e é possível extrapolar o uso da ferramenta, tornando, portanto, sua construção mais complexa. Hoje, trabalharemos com exemplos simples, no intuito de compreender o funcionamento da ferramenta. Assim, para construir um fluxograma, precisamos:

1. Fazer a coleta de dados: precisamos reunir medições daquilo que queremos analisar. Esses dados podem ser de uma nova coleta ou já coletados anteriormente;
2. Definir o número de faixas e os limites: aqui, agrupamos os dados em intervalos específicos e lógicos, delimitando também os limites Superiores e Inferiores. Vale dizer que existem regras que podem ajudar nessa definição (Fórmula de Sturges ou a Raiz Quadrada, por exemplo), mas também podemos fazer isso analisando o processo e o contexto;
3. Contar a frequência de ocorrência entre intervalos: com os dados agrupados, identifique quantas vezes cada dado se repete em cada faixa;
4. Construir a tabela de frequências: aqui, organizamos todos os dados em uma tabela, facilitando assim o uso e montagem do Histograma; 
5. Montar o gráfico de barras: coloque as faixas (intervalos) no eixo X e a frequência no eixo Y. Dessa forma, cada barra criada representará os intervalos e a altura a frequência em que os dados ocorreram;
6. Interpretar o gráfico: tudo pronto, basta analisar o gráfico como fizemos no capítulo “Interpretando um histograma”.

Exemplo de construção do gráfico de distribuição de frequências

Relembre o exemplo que utilizamos acima (número de peças com tamanho não conforme em milímetros). Para construí-lo, primeiramente nós precisamos coletar os dados. Imagine, então, que esses os coletamos após o Controle de Qualidade recusar as 500 peças defeituosas.

Na Frequência Absoluta

Com os dados em mãos, separamos os defeitos em intervalos. Eu decidi separá-los em 5 faixas (com cerca de 1 milímetro de divergência em cada faixa). Depois, contamos a frequência em que cada defeito ocorreu. Assim, construímos a seguinte tabela:

Faixa de defeito (mm)	Frequência absoluta (peças)
< 2 mm	50
2 – 3 mm	100
3 – 4 mm	250
4 – 5 mm	70
> 5 mm	30
Total	500

Agora, colocamos a frequência no eixo Y e as faixas no eixo X.

Depois, construímos as barras. ou seja, na faixa de “<2 mm”, por exemplo, vamos subir a barra até 50, afinal esse é o número de peças que apresentaram essa não conformidade. Já na faixa “4 – 5 mm”, por exemplo, vamos subir a barra até o 70, ou seja, usando o número de peças que apresentarem esse defeito de tamanho. 

Fazendo isso para todas as faixas, voilà, teremos o gráfico pronto:

Na Frequência Relativa

Caso você queira o gráfico da Frequência Relativa (%), basta adaptar a tabela com as porcentagens ao invés do número bruto. Então é só repetir o processo de construção das barras. Dessa forma, a tabela ficaria assim: 

Faixa de defeito (mm)	Frequência relativa (%)
< 2 mm	10%
2 – 3 mm	20%
3 – 4 mm	50%
4 – 5 mm	14%
> 5 mm	6%
Total	100%

Após isso, é só refazermos o gráfico e teremos as seguintes barras:

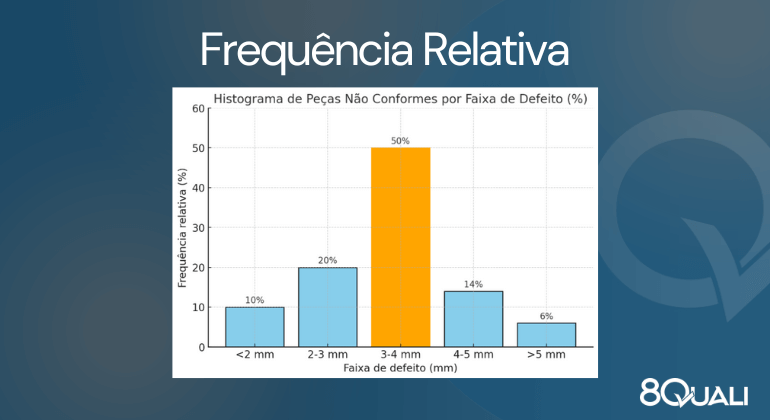
Agora, conseguimos compreender, por exemplo que “70% dos defeitos estão concentrados entre 2 e 4 mm”. Ou então, percebemos que “16% dos defeitos estão abaixo dos 2 mm ou acima dos 5 mm”.

Ambas as interpretações são as “mesmas” da versão anterior, com os mesmos resultados e “os mesmos números”. Entretanto, aqui, temos o viés percentual. Qual das duas usar? Expliquei isso lá no capítulo “Entendendo frequência ABSOLUTA ou RELATIVA”.😉

Aprofundando seus estudos [Material para Download]

Se você quiser aprender um pouco mais sobre Histograma, o pessoal do 8Quali tem um material muito legal para download. O “Guia Montando seu Histograma” traz um exemplo um pouco mais aprofundado, elaborado, com uma amostra de coletas destrinchada e fórmulas matemáticas.

Inclusive, o material possui outras dicas de como interpretar os resultados do Histograma, afinal o desenho formado pelas colunas pode te dizer muita coisa! O exemplo dele é uma pouco mais complexo, o que ajuda a entender novas formas de análise. Por exemplo, é possível que o gráfico tenha 2 picos de dados, o que isso pode significar? Baixe o conteúdo e descubra!

Clique no botão abaixo para baixar gratuitamente e aprender ainda mais sobre essa ferramenta incrível! 👊🏻😉

Baixar Conteúdo Gratuito

Interpretando a história, moldando o futuro!

Muitas vezes, interpretar grandes conjuntos de dados é uma tarefa árdua, complexa e até mesmo chata. Afinal, olhar para uma folha com 500, 1000, 1500 coletas é sem graça e difícil. Raras são as pessoas que conseguem compreender padrões apenas dessa forma. Olhando para um monte de números enfileirados. Eu, particularmente, só me lembro do Sheldon, da série The Big Bang Theory, e ele é um personagem fictício! 😅

O pior de tudo é que grande parte da história de nossas empresas existe apenas em algumas centenas de números. São dados, estatísticas, porcentagens, coletas, páginas e mais páginas de algarismos e cifras. Assim, ao sermos incapazes de compreender esses dados brutos, somos também incapazes de compreender grande parte do que fazemos. É neste aspecto que residem, muitas vezes, as falhas, os problemas e até mesmo as falências.

E, a meu ver, não tem nada mais triste do que uma empresa que “encerra sua história”… Por isso, para mim, o Histograma se destaca de 2 formas:

• Primeiro, porque nos ajuda a navegar nesse emaranhado numérico, encontrando sentidos e direções;
• Segundo, porque ele nos ajuda a mostrar os resultados (e interpretações) para outras pessoas, facilitando o entendimento de ainda mais pessoas.

O Histograma é, portanto, não só uma ferramenta de análise, mas também de comunicação e diálogo, pois não nos engajamos no que não entendemos. A partir dele, podemos descobrir e implementar otimizações, fazer correções, evitar reincidências e retrabalhos, ou seja: podemos melhorar as coisas. Dessa forma, com ele, não só entendemos o passado como moldamos os resultados do futuro!